Euler, e sayısını ilk kez 1683 yılında, logaritmalar üzerine çalışırken keşfetmiştir. Bu sayı, matematiksel hesaplamalarda sıkça karşılaşılan ve çok önemli bir sabittir. Ancak, bu sayının gerçekten popülerleşmesi, Leonhard Euler tarafından matematiksel anlamının derinlemesine incelenmesiyle olmuştur. Euler, e'yi bir limit olarak tanımlamıştır ve bu tanım şöyle ifade edilir
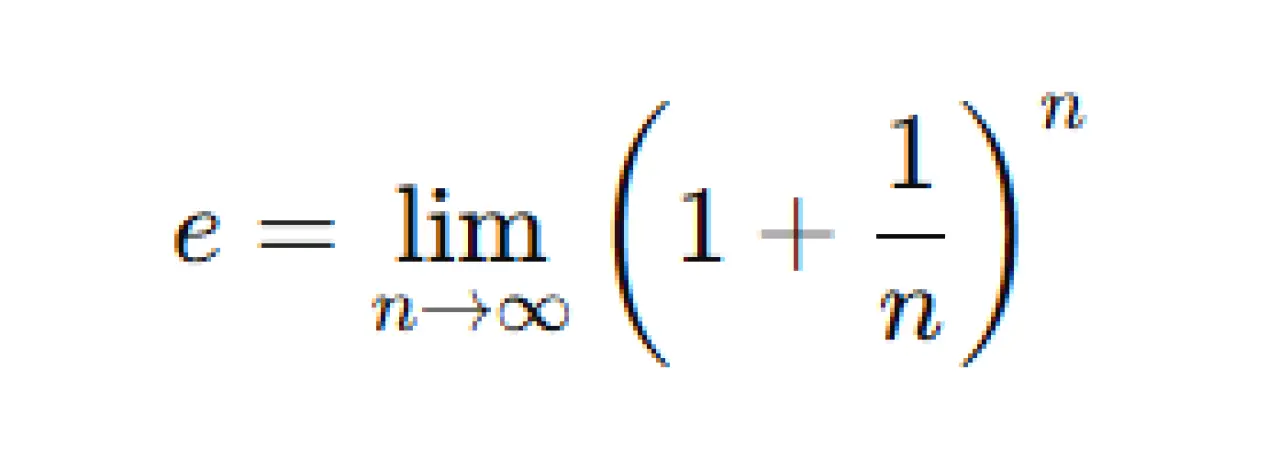
Bu ifade, e'yi sürekli büyüyen bir oran olarak tanımlar. Başka bir ifadeyle, her defasında birim bir artışa sahip bir sayının sınırsız sayıda tekrarından elde edilen limit değerini belirtir.
e Sayısının Matematiksel Özellikleri
e ≈ 2.71828... olarak bilinir ve sayısal bir değeri vardır.
e, matematiksel analizde, özellikle türev ve integral hesaplamalarında kullanılır.
Bu sayı, özellikle logaritmalar, diferansiyasyon, ve sürekli büyüme ile ilgili problemlerde önemli bir rol oynar.
e Sayısının Kullanım Alanları
Sürekli Büyüme ve Azalma:
e sayısı, sürekli büyüyen ya da azalan sistemlerin modellenmesinde kullanılır. Örneğin, bankacılıkta bileşik faiz hesaplamaları sürekli büyüyen bir modelle yapılır ve burada e kullanılır.
Nüfus artışı, bakteri çoğalması gibi biyolojik süreçler de sürekli büyüme gösterdiği için e ile modellenebilir.
Matematiksel Finans Hesaplamalarında Kullanılır
Finans dünyasında, özellikle bileşik faiz hesaplamalarında e sayısı kullanılır. Yatırımın zaman içinde nasıl büyüdüğünü anlamak için e'nin gücü gereklidir.
Logaritma ve Üstel Fonksiyonlarda Kullanılır
Natural logaritmalar (ln) ve üstel fonksiyonlar (e^x) gibi fonksiyonlar da e sayısı ile bağlantılıdır. Bu fonksiyonlar, birçok doğal olayın modellenmesinde kullanılır.
Fizik ve Mühendislik Alanlarında Kullanılır
e, özellikle elektrik mühendisliği, kuantum mekaniği gibi fiziksel ve mühendislik uygulamalarında da sıkça kullanılır.
Euler'in e sayısının temel özellikleri ve kullanım alanları, matematiksel ve fiziksel birçok problemi çözmede kritik bir rol oynar.



















